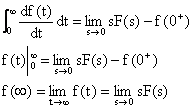自动控制网移动版

拉氏变换是控制工程中的一个基本数学方法，其优点是能将时间函数的导数经拉氏变换后，变成复变量S的乘积，将时间表示的微分方程，变成以S表示的代数方程。

一、拉氏变换与拉氏及变换的定义

1、拉氏变换：设有时间函数，其中，则f(t)的拉氏变换记作：

称L—拉氏变换符号；s-复变量； F(s)—为f(t)的拉氏变换函数，称为象函数。

f(t)—原函数

拉氏变换存在，f(t)必须满足两个条件(狄里赫利条件)：

1)在任何一有限区间内，f(t)分断连续，只有有限个间断点。

2)当时，，M，a为实常数。

2、拉氏反变换：将象函数F（s）变换成与之相对应的原函数f(t)的过程。

—拉氏反变换符号

关于拉氏及变换的计算方法，常用的有：①查拉氏变换表；②部分分式展开法。

二、典型时间函数的拉氏变换

在实际中，对系统进行分析所需的输入信号常可化简成一个成几个简单的信号，这些信号可用一些典型时间函数来表示，本节要介绍一些典型函数的拉氏变换。

1．单位阶跃函数

2．单位脉冲函数

3．单位斜坡函数

4．指数函数

5．正弦函数sinwt

由欧拉公式：

所以，

6．余弦函数coswt

其它的可见表2-1：拉氏变换对照表

三、拉氏变换的性质

1、线性性质

若有常数k₁，k₂,函数f₁(t),f₂(t),且f₁(t),f₂(t)的拉氏变换为F₁(s),F₂(s),

则有：，此式可由定义证明。

2、位移定理

(1)实数域的位移定理

若f(t)的拉氏变换为F(s),则对任一正实数a

有, 其中，当t<0时，f(t)=0，f(t-a)表f(t)延迟时间a.

证明：，

令t-a=τ,则有上式=

例：, 求其拉氏变换

(2)复数域的位移定理

若f(t)的拉氏变换为F(s),对于任一常数a,有

证：

例：求的拉氏变换

3、微分定理

设f(t)的拉氏变换为F(s),

则

其中f(0⁺)由正向使的f(t)值。

证：

同理可推广到n阶：

当初始条件为0时，即

则有

4、积分定理

设f(t)的拉氏变换为F(s),则

，其中时的值。

证明：

同理可得n阶积分的拉氏变换：

当初始条件为0时，f(t)的各重积分在时，均为0，则有

    ]

5、初值定理

设f(t)的拉氏变换为F(s)，则函数f(t)的初值定理表示为：

证明：由微分定理知：

对等式两边取极限：

则有

例：已知 ，求f(0⁺)

由初值定理知：

6、终值定理：

若f(t)的拉氏变换为F(s),则终值定理表示为：

证明：由微分定理知：

令，对上式两边取极限，

这个定理在稳态误差中常用。

例：已知：，求f()

7、卷积定理

设f(t)的拉氏变换为F(s),g(t)的拉氏变换为G(s)，

则有

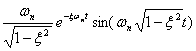
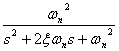
式中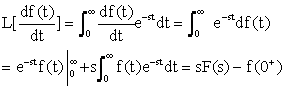，称为f(t)与g(t)的卷积。此定理不要求证明。