|
|
 |
1. 典型I型系统
① 结构图与传递函数 |
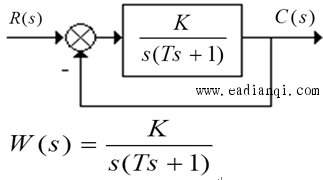 |
式中 T — 系统的惯性时间常数
(系统固有,不变);
K — 系统的开环增益(可变)。
② 开环对数频率特性 |
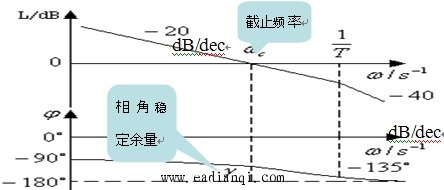 |
③ 性能特性
典型的I型系统结构简单,其对数幅频特性的中频段以–20 dB/dec 的斜率穿越 0dB 线,只要参数的选择能保证足够的中频带宽度,系统就一定是稳定的,且有足够的稳定裕量,即选择参数满足 |
 或 或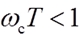 |
|
于是,相角稳定裕度 |
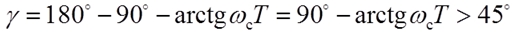 |
对于给定作用的跟随性是一阶无静差,σ%较小,但抗扰能力稍差。
2.典型Ⅱ型系统
① 结构图和传递函数 |
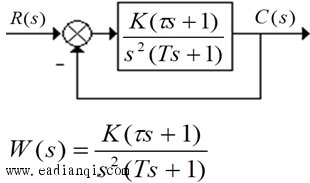 |
是Ⅱ型系统中最简单且稳定的结构。许多采用PI调节器的调速系统和随动系统都可以成这种结构形式。
② 开环对数频率特性 |
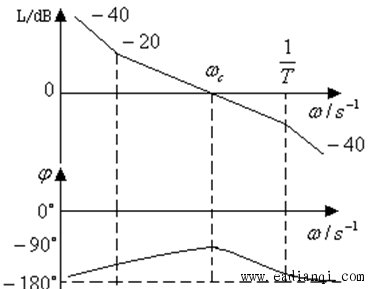 |
 |
 或 或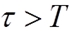 |
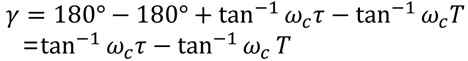 |
 |
对于给定作用的跟随性是二阶无静差,而且可以得到比较好的抗扰性能,但 σ% 较大。
典型I型系统跟随性能指标和频域指标与参数的关系
(ξ与KT的关系服从于式(*)) |
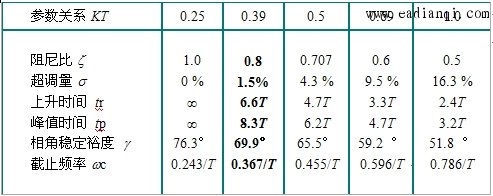 |
具体选择参数时,应根据系统工艺要求选择参数以满足性能指标。
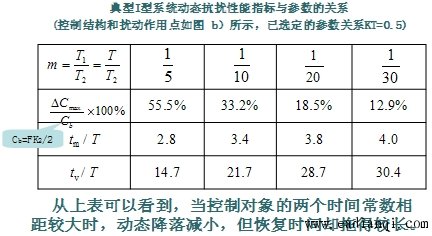
典型I型系统抗扰性能指标与参数的关系
(1)稳态抗扰性能指标:由于扰动输入为阶跃信号,其输出为无静差。即,系统受扰后可完全恢复。
(2)动态抗扰性能指标
典型 I 型系统 |
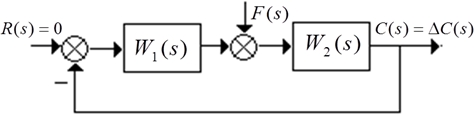 |
扰动 F 作用下的典型 I 型系统 a)
上图是在扰动 F 作用下的典型 I 型系统,其中,W1 (s)是扰动作用点前面部分的传递函数,后面部分是W2 (s) 。
在一个系统中,扰动作用点是不同的,某种定量的抗扰性能指标只适用于一种特定的扰动作用点。因此,分析抗扰性能指标较复杂。
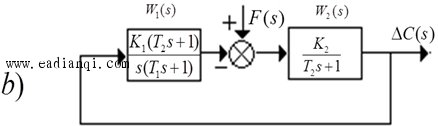
在此只分析W1 (s)、W2 (s) 各是一种特定形式的抗扰性能,其它情况可仿此处理。 |
 |
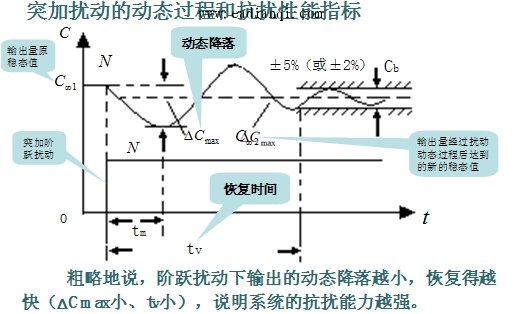
 |